子供たちが夢中になる、仮面ライダーやウルトラマンの変身ベルト。「いつか自分だけの変身ベルトを作ってみたい!」って、きっと誰もが一度は思ったことがあるはず。
今回は、そんな夢をちょっぴり科学の力で実現するプロジェクトに挑戦!ただ光るだけじゃなく、「触れるとチャージが始まって、しばらくすると光る!」という、まるで魔法みたいな変身ベルトの プロトタイプを作ってみることにしました。
実はこれ、以前から試してみたかった「手回し発電機」の応用がきっかけ。手でぐるぐる回すとゲージが溜まって光るベルト…って想像するだけでもワクワクしますよね!
でも、工作用のモーターを発電機として使う場合、満足な電気を作るには結構速く回さないといけない。腰につける変身ベルトには、ちょっと大きすぎるしかさばりそう…。
そこで、手回し発電は一旦保留にして、別のチャージ方法を考えることに。そんな時、以前読んで面白かった本「Make: Electronics – 作ってわかる電気と電子回路の基礎」に書いてあった、「指で触ることでトランジスタを動かす」というアイデアが不意に浮かんできたんです!
これだ!普段は何も起こらないのに、触ることで電気の流れが始まってチャージされる仕組みなら、変身ベルトのサイズにも収まるし、何より子供でも簡単に使える!
というわけで、まずは簡単な実験からスタート!トランジスタとコンデンサ、LEDを使って、「触るとトランジスタがONになって電気のチャージが始まり、ある程度の時間が経つとLEDが光る」という動作を、本当に実現できるのか試してみました。
実験回路 – 指先が魔法のスイッチ!?
最初に考えたのは、図1のような回路。これは、指で触ることで電気の流れを作り出す、ちょっと変わったな仕組みです。
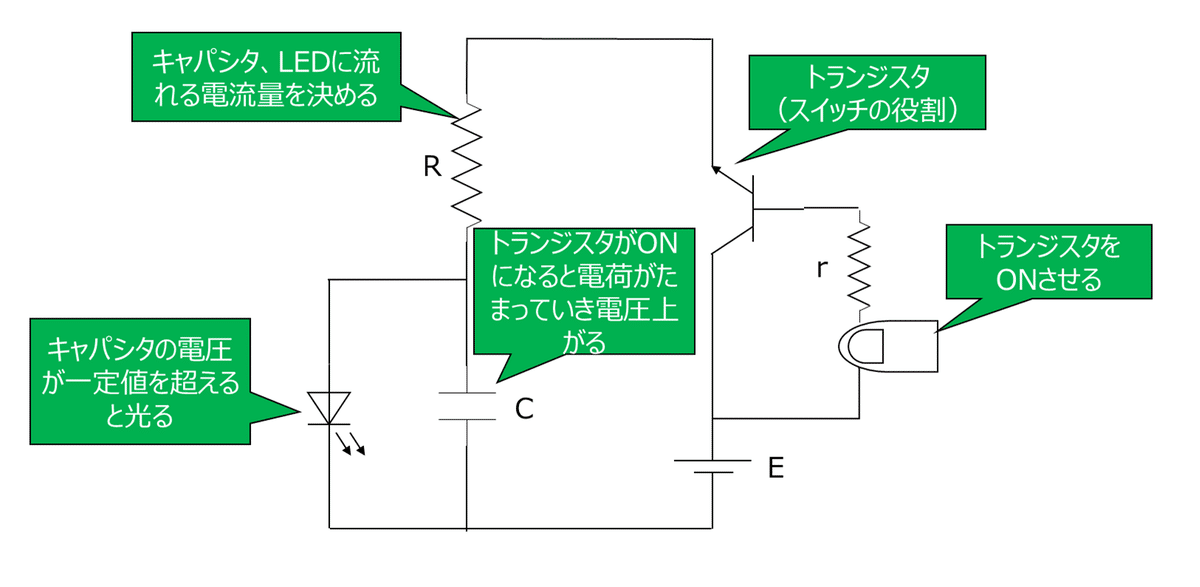
指先マークのところに、湿った指でそっと触れると…
⇒ トランジスタのベースという部分に、ごくわずかな電気が流れて、トランジスタがONの状態になる!
⇒ すると、コレクタという部分から電気が流れ出し、コンデンサという部品に電気が溜まり始める(これを「チャージ」と呼びます)。同時に、LEDにかかる電圧も上がっていくんです(コンデンサとLEDは電気の流れを共有しているんです)。
⇒ そして、LEDが光り始めるために必要な電圧を超えると…ついに、LEDが点灯する!
言葉で説明すると、なんだか単純な回路と動作原理に見えるかもしれませんが、実際にアイデアを形にするのは、まるでパズルを組み立てるみたいに興味深いプロセスなんです!
パラメータ設定 – 「しばらくすると光る」 タイマーの秘密
時定数の考え方
この変身ベルトの最大のポイントは、触ってすぐに光るのではなく、「しばらくすると」光るという「時間差」があること!この「時間遅れ」をどうやって作り出すかが、この電気工作の面白いところです。
そこで活躍するのが「時定数」という考え方。これは、電気回路で電気が溜まったり流れ出たりする速さの目安になるものです。図1の抵抗RとコンデンサCを使うと、時定数(τ)は、
τ=R×C
というシンプルな式で表せるんです。難しく考えなくても大丈夫!ここでは、「電気のチャージや 放出にかかる時間の目安」くらいのイメージでOKです。
「目標とする時間遅れに合わせて、抵抗RとコンデンサCの値を決めよう!」と考えたいところですが…ここで 予想外の壁が!
キャパシタンスの値 – 手持ちの部品を創造的に活用!
手元にあるコンデンサの種類が、思ったよりも少なかったんです(笑)。つまり、「理想の時定数に合わせてRとCを選ぶ」のではなく、「今あるコンデンサを最大限に活かして、抵抗Rで時定数を調整する」というクリエイティブな戦略に変更せざるを得ませんでした。
手元にあったのは、100μF(マイクロファラッド)が3つ、220μFが3つ、そして1000μFが1つ。コンデンサは、並列に繋ぐほど電気を溜めるキャパシタンスが大きくなるので、持っているコンデンサを全部並列に繋ぐことに!その結果、合計で1960μF、つまり1.96mF(ミリファラッド)になりました。
「コンデンサのキャパシタンスが決まったなら、あとはほしい時定数に合わせて抵抗を選べばいいのでは?」と思うかもしれません。でも、抵抗を大きくしすぎると、電気の流れが小さくなって、LEDが光らない可能性があるんです。
抵抗値 – 光と時間、電気バランスのアート
だから、「ある程度の時間遅れを作る」と「LEDをちゃんと光らせる」という2つの要求を両立させる、ちょうどいい抵抗値を見つける必要があります。
LEDがどのくらいの電流で、どのくらいの明るさで光るかは、以前の実験で確認済み!だいたい4mA(ミリアンペア)程度の電流を流せば、はっきりと光ることが分かりました(ただし、LEDの色によって電流と電圧の関係は少し変わるので注意が必要です)。
では、図1の回路でLEDに4mAの電流を流すためには、抵抗Rはどのくらいの値に設定すればいいでしょうか?
コンデンサへのチャージが完了した状態では、コンデンサには電流が流れなくなるので、LEDに流れる 電流は、抵抗Rに流れる電流と同じになります。そこで、抵抗Rに4mAの電流を流すために、抵抗Rの値を計算します。
電気の基本法則「オームの法則」(V = I × R)を使うと、抵抗にかかる電圧(V)が分かれば、抵抗値(R)を計算できます。LEDにかかる電圧をVLED、抵抗Rにかかる電圧をVRとすると、電気回路の基本法則「キルヒホッフの法則」から、電源の電圧Eは、
$${E=V_{LED}+V_R}$$となります。
今回使った黄色のLEDの動作電圧は約2V、電源は余っていた単3乾電池4本を直列に繋いで4.93Vだったので、抵抗にかかる電圧VRは、
$${V_R=E-V_{LED}=4.93-2.00=2.93}$$
となります。ここに4mA(0.004A)の電流を流すためには、抵抗Rは、
R=VR/I=2.93V/0.004A=732.5Ω
となります。手元にぴったりの抵抗がなかったので、近い値のR=680Ωを使うことにしました。ちなみに、トランジスタのベースに繋ぐ抵抗rの値は、100Ωに設定しました。
実際の動作 – 光るけれど、ちょっと期待外れ?
LEDは光るのだが・・・
こちらが、LEDに680Ωの抵抗を直列接続した時のLEDの点灯動画です。
変身ベルトですから!
やっぱり、「ジワー…」っと溜まって、「バーン!」と光る、あの「溜め」の演出が欲しいじゃないですか!
τ=R×C
なので、もっと抵抗Rの値を大きくする必要がありそうです。
時定数とLED輝度の微妙なバランス- 遅れる光、でも輝きは?
そこで、抵抗Rの値を2200Ωに変えて実験してみました(rは100Ω、Cは1.96mF、Eは4.93V)。その 動画がこちら!
今度は、「溜め」の感じがそこそこ表現できているように思います!
ただ…ちょっと光が弱い?
抵抗を大きくすると電流の流れが弱くなって光が暗くなるし、抵抗を小さくすると時間遅れが短くなってしまう。「あちらを立てればこちらが立たぬ」状態です。
理想はバランスが取れた状態ですが、今回どちらかを選ぶとしたら、やはり「点灯の遅れ」の方を優先したい!輝度の方は、とりあえず光っていることが分かればOKとします。
時定数はどのくらい? – 計算と体感の不一致?
ところで、Rを680Ωにした場合と2200Ωにした場合、それぞれの時定数はどのくらいだったのでしょうか?
τ=R×C なので、
- R = 680Ωの場合: τ=680Ω×(1.96×10−3F)=1.3秒
- R = 2200Ωの場合: τ=2200Ω×(1.96×10−3F)=4.3秒
実際に動画で見た点灯の遅れよりも、計算した値の方が少し大きく感じるかもしれませんが、だいたいの目安としては妥当な範囲かなと思います。
まとめ – 指先チャージ式!時間差で光る変身ベルトプロトタイプ完成!
今回の実験では、触れただけで電流がチャージされ、数秒の遅れを持ってLEDが光るという、変身ベルトの基本的な仕掛けを プロトタイプしてみました。
コンデンサと抵抗の値を 創造的に組み合わせることで、 ほしい時間遅れを作り出すことができるんですね!
手持ちのコンデンサを最大限に活用したせいで配線が少しごちゃついてしまいましたが、最初から静電容量の大きなコンデンサを用意しておけば、もっとスッキリした回路にできるはずです。
次は、この仕組みを応用して、変身ベルトのゲージが順々に上がっていくような、より本格的な仕掛け作りに挑戦してみたいと思います!


