はじめに:レストランで活躍する自律移動ロボットのセンサー技術
最近のファミレスでは、自律移動ロボットが配膳するのが当たり前になってきました。はじめは、こんなもん普及するかよと高をくくっていましたが、あれよあれよという間に大量導入が進んでいきました。たまに店員さんに回収される猫型ロボットのほほえましい姿を目にしはするものの、概して良い仕事をしているみたいです。
これらのロボットがスムーズに店内を移動し、障害物を回避しながら正確に料理を届けるためには、周囲の状況を認識するためのセンサーが不可欠です。本記事では、その「視覚」の一端を担う可能性のある、シャープの測距モジュール GP2Y0A21YK について、その基本的な原理から特性、応用までを解説します。
測距センサーGP2Y0A21YKの距離測定原理:三角測距と幾何学
GP2Y0A21YK が距離を測定する基本的な原理は 三角測距法 です。中学数学で「一辺両端角相等」というのをやったことを覚えているでしょうか。三角形の一辺の長さと、その両端の角度が一緒であれば、2つの三角形は合同というやつです。あれを使います。次の図をみてください。
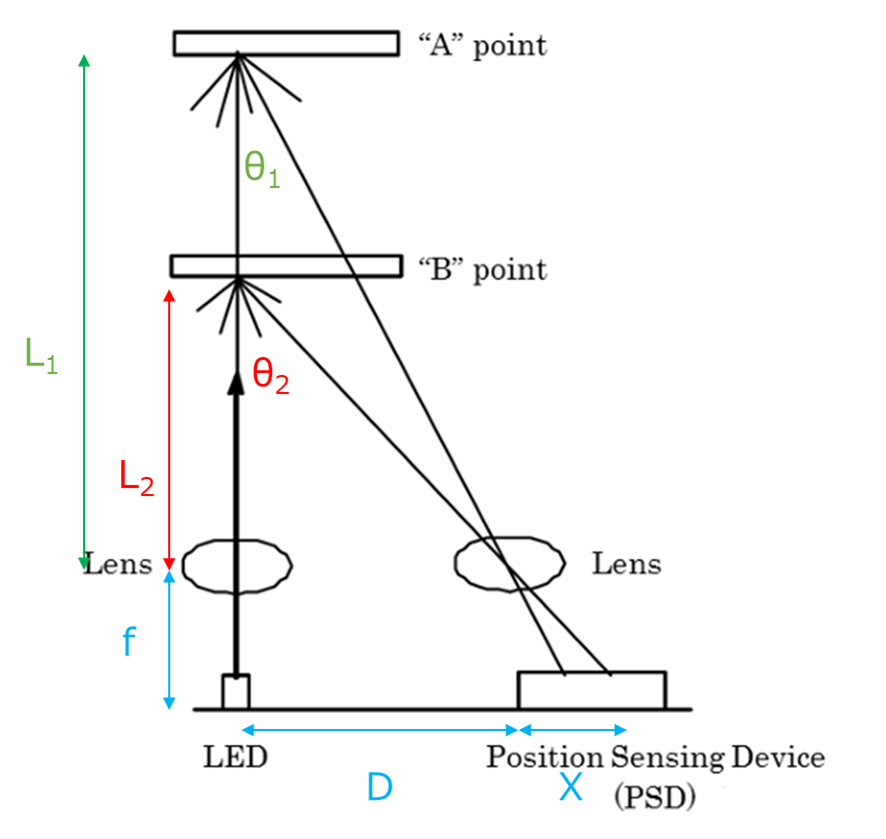
この図で、測定したいのは、レンズからA、あるいはB点までの距離L1、L2です。図のように${\theta_1}$、${\theta_2}$をおくと、Lは$${L=\frac{D}{tan\theta}}$$で表せます。ですが、θは直接は測定できません。そこで、レンズの焦点距離fと、反射光が受光素子に結像する位置のレンズ中心からのずれXを使って、$${tan\theta=\frac{X}{f}}$$で置き換えLを計測します。
データシートは数理モデルの宝庫:特性グラフと近似関数
GP2Y0A21YK のデータシートには、測定距離と出力電圧の関係を示すグラフが掲載されています。
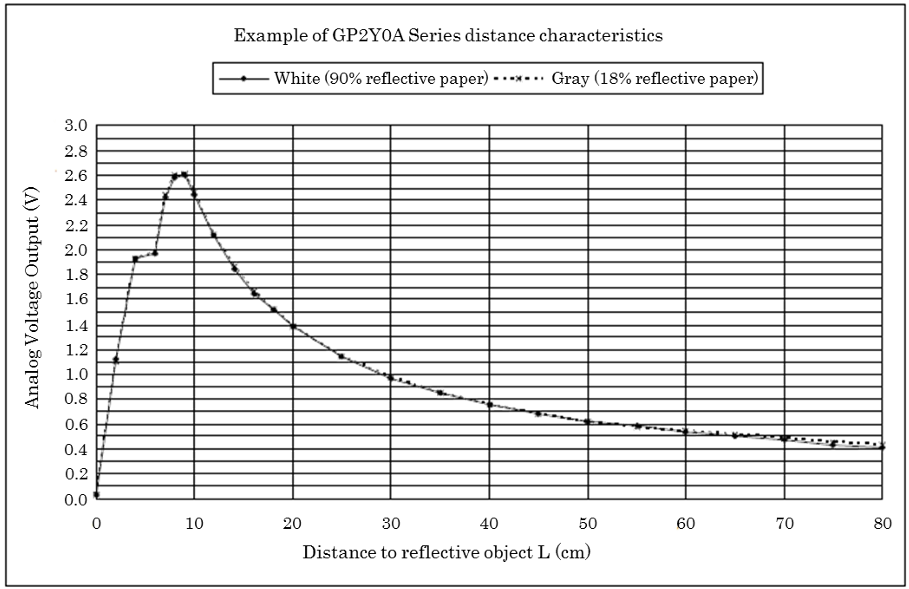
このグラフは、センサーの挙動を示す重要な 数理モデル と捉えることができます。
- 非線形な特性: 多くの距離センサーと同様に、GP2Y0A21YK の出力電圧と距離の関係は一般的に非線形です(線形=直線ではない)。これは、単純な比例関係(直線)では表現できない、より複雑な関数によって記述されることを意味します。
- 近似関数の重要性: マイコンで距離を算出するためには、この非線形な特性を数学的な関数で近似する必要があります。なぜなら、実際にこの測距センサーで得られる測定値はあくまで電圧(グラフの縦軸)なのであって、これを距離(横軸)に変換する部分は自分でやる必要があるからです。なので、データシートのグラフから適切な関数形(指数関数、対数関数、多項式など)を選択し、実験データに基づいてそのパラメータを決定する 関数フィッティング の技術が重要となります。
- 誤差評価: 近似関数を用いる際には、元の特性グラフとの間に必ず誤差が生じます。この誤差の範囲を理解し、実際のアプリケーションにおける精度を評価することも、数学的な視点から重要な要素です。
測定精度に影響を与える数学的要因
GP2Y0A21YK の測定精度は、様々な要因によって影響を受けますが、その多くは数学的に分析することができます。
- 分解能: センサーが出力するアナログ電圧の分解能は、測定できる距離の最小単位に影響を与えます。これは、アナログ-デジタル変換器(ADC)のビット数によって決定されます。
- ノイズ: 電気的なノイズは、測定値のばらつきを引き起こします。統計的な手法を用いてノイズの影響を評価し、フィルタリングなどの処理を施すことが重要になります。
- 環境要因のモデル化: 測定対象物の反射率や周囲の環境光、温度といった要因が測定値に与える影響を数学的にモデル化し、補正することも高度な応用では検討されます。
まとめ:数学的視点で GP2Y0A21YK の可能性を拓く
いまの時代はテクノロジーが発達していて、「非接触で距離を測る」なんて言ったところで驚くような人はそういないでしょう。ですが、その測定原理に、実は中学数学程度で学んだ内容が応用されていることなどを知ると、改めてその技術に親近感を覚えたり、深遠さを感じられたりするのではないでしょうか。
データシートを単なる仕様書の羅列として捉えるのではなく、数理モデルの宝庫として読み解き、数学的な視点からその特性を理解することで、より高度な応用や問題解決に繋げることができるでしょう。


