はじめに
富士山が大規模噴火したときの降灰シミュレーションが、今年8月に内閣府から公開されました。
25km、60km、100kmと、距離による降灰の違いが示されており、誰もが想像できるように、火口に近いほど灰の堆積が大きくなります。
少し前に書いた以下の記事では、ごみ処理場の煙突の高さについて触れました。
煙突を高くするのは、地上における汚染物質の濃度を安全レベルにまで「希釈」するため。
つまり、煙やガスが大気中で「広がる」性質をうまく利用しているわけです。
今回はこの「広がり」――すなわち“拡散”を、数学の目で見てみます。
テーマは「大気中の煙の広がり」と、それを支配する法則です。
フィックの第1法則 ― 流れを生む勾配
ドイツの物理学者アドルフ・フィックは、物質が拡散していく現象を「流れ」としてとらえました。
濃度が高いところから低いところへ物質が移動していく――この流れ(フラックス) J は、濃度の変化率(勾配)に比例する。それを表すのが次の式です。
$${J=-D\frac{dC}{dx}}$$
ここで
- J [mol/m²·s]:単位面積あたりの物質流量
- D [m²/s]:拡散係数(物質や媒質によって決まる)
- C [mol/m³]:濃度
- x [m]:位置
負の符号は「濃いほうから薄いほうへ流れる」ことを意味しています。
図にすればこんな感じです。
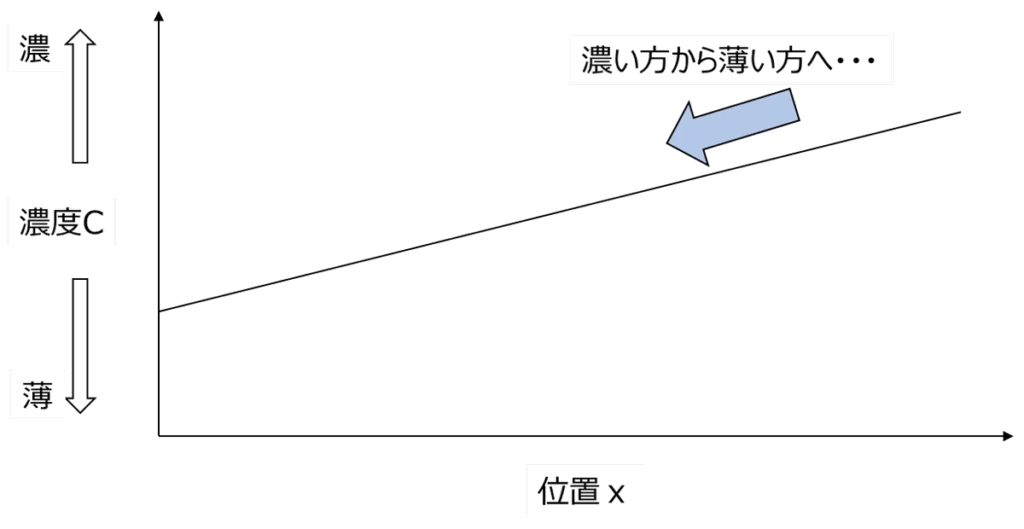
言い換えれば、濃度差があるところに流れが生じる。
このシンプルな一行が、後に登場する「拡散方程式」の出発点になります。
まとめ
- 物質の流れは「濃度の勾配」に比例する。
- 流れの向きは、濃度が高い方から低い方へ。
- この考えが、次に扱う「時間変化(第2法則)」につながっていく。
次回は、この「流れ」が時間とともにどのように変化していくか――
つまり、「拡散方程式」と呼ばれる微分方程式の世界を見ていきます。


