前回は「濃度差が流れを生む」というフィックの第1法則を紹介しました。
今回はその流れが時間とともにどう変化していくかを表す、第2法則に踏み込みます。
フィックの第2法則 ― 時間とともに変わる濃度
流れが生じて物質が移動するということは、もとの場所の濃度が変化していくということです。
これは、人が混雑した車両から空いている車両へ移っていくとき、中央の混雑がだんだん緩和されていくのに似ています。
この現象を表すのが「拡散方程式」です。
${\frac{\partial C}{\partial t} = D \frac{\partial^2 C}{\partial x^2}}$ … 式(1)
左辺は濃度の時間変化(時間微分)、つまりある位置での濃度が時間とともにどう変わっていくか、その変化率を表します。
一方、右辺は濃度変化の変化率(濃度の2階微分)、つまりその位置が濃度変化のさらにキツくなっている点なのか、濃度変化が緩やかになっている点なのかを表します。
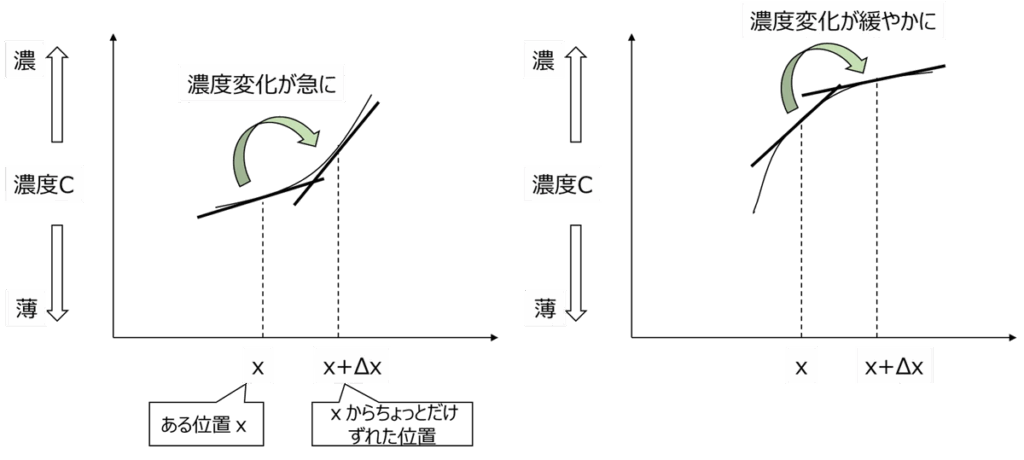
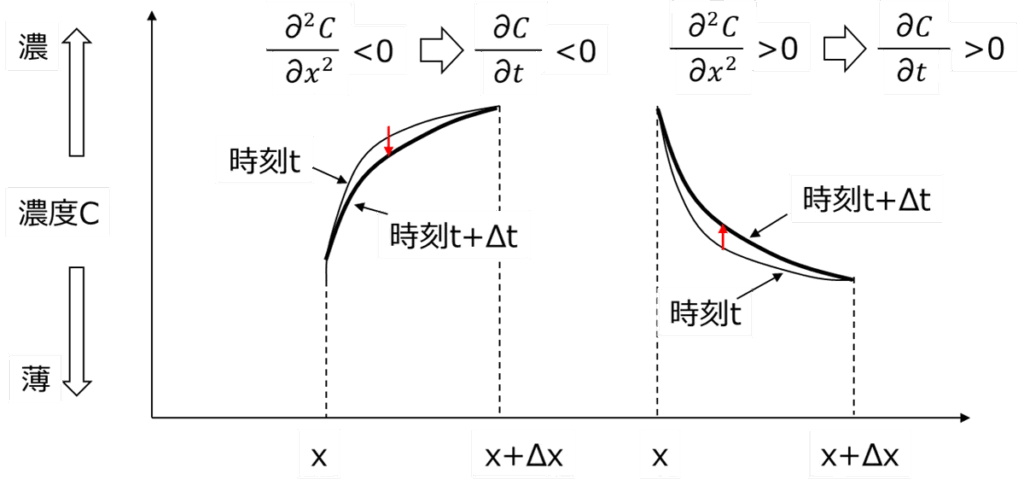
右辺がプラスの場合、マイナスの場合に何が起こるか、端的に図で表すと次のようになります。
方程式を解く ― 変数分離法の一例
この偏微分方程式を解くために、次のような仮定を置きます。
${C(x,t)=T(t)X(x)}$ … 式(2)
T(t)は時間だけに依存して位置に依存しない関数、 X(x)は逆に位置だけに依存して時間に依存しない関数を表します。すると、式(2)は次のように書けます。
${\frac{T}{∂t}X=DT \frac{∂^2 X}{∂x^2}}$ … 式(3)
左辺をtのみの関数、右辺をxのみの関数となるよう式変形すると
${\frac{1}{T} \frac{T}{∂t}=D\frac{1}{X} \frac{∂^2X}{∂x^2}}$ … 式(4)
この式を解釈するポイントは、この式(4)は「どんなx、tの値でも成り立つ必要がある」ということです。
左辺はtだけの関数なので、tの値が変われば、うにゃうにゃ値が変わるはずです。
一方右辺の方もxだけの関数なので、tの値とは関係ないところで、xの値が変わればそれに応じてうにゃうにゃ値が変わるはずです。
にも関わらず右左辺が等号で結ばれているということは、どんなx、tの値を代入したところで、左辺も右辺も値は変わらないよということです。つまり、定数です。これを${\alpha}$とおくと
${\frac{1}{T} \frac{T}{∂t}=D\frac{1}{X} \frac{∂^2X}{∂x^2}=\alpha}$ … 式(5)
となります。これを2つの式に分解してみます。
${\frac{1}{T} \frac{T}{∂t}=\alpha}$ … 式(6)
${D\frac{1}{X} \frac{∂^2X}{∂x^2}=\alpha}$ … 式(7)
式(6)は1階線形常微分方程式、式(7)は2階線形常微分方程式と呼ばれるものです。これらは、理系学部なら必ず扱うはずのもので、参考書でもネット上でも、方法が簡単に調べられるので、トライしてみてください。
結論だけかくと、式(6)、(7)に対する解はそれぞれ以下のようになります。
${T(t)=Aexp(\alpha t))}$ ー 式(8)
${X(x)=Bcos(−\frac{D}{\alpha} x)+Csin(−\frac{D}{\alpha} x)}$ ー 式(9)
これらを式(2)に代入すると
${C(x,t)=Aexp(\alpha t)\{Bcos(−\frac{D}{\alpha} x)+Csin(−\frac{D}{\alpha} x)\}}$ ー 式(10)
となり、式(1)の拡散方程式の解となります。
2階線形常微分方程式の解の形にはいくつかパターンがあるのですが、今回の場合、結果的に式(10)のように三角関数が現れる形となります。その理由については、たとえば資料[1]が参考になると思います。
式を読む
式(10)は一見複雑な形をしていますが、「骨格」だけ捉えると、式(8)の指数関数と、式(9)の三角関数の積という形をしています。
さらに言うと式(9)は、高校で学ぶ三角関数の合成を使いたくなってしまう形をしています。詳しくは、資料[2]など参照し、雰囲気を思い出してみてください。
要するに、cosとsinの和の形で表されていますが、ひとつのsin、またはcosの形で表せるということです。
さて、式(10)をどう眺めるかということですが、大きく分けて「時間が経ったらどうなるか」「位置が変わったらどうなるか」の2つで見ると、実際の現象と整合しているか、をざっと確認できます。
1. 時間が経ったらどうなるか
まず、時間については、式(10)の中でも
${Aexp(\alpha t)}$に集約されているので、この関数の振る舞いだけに注視すればよいのです。
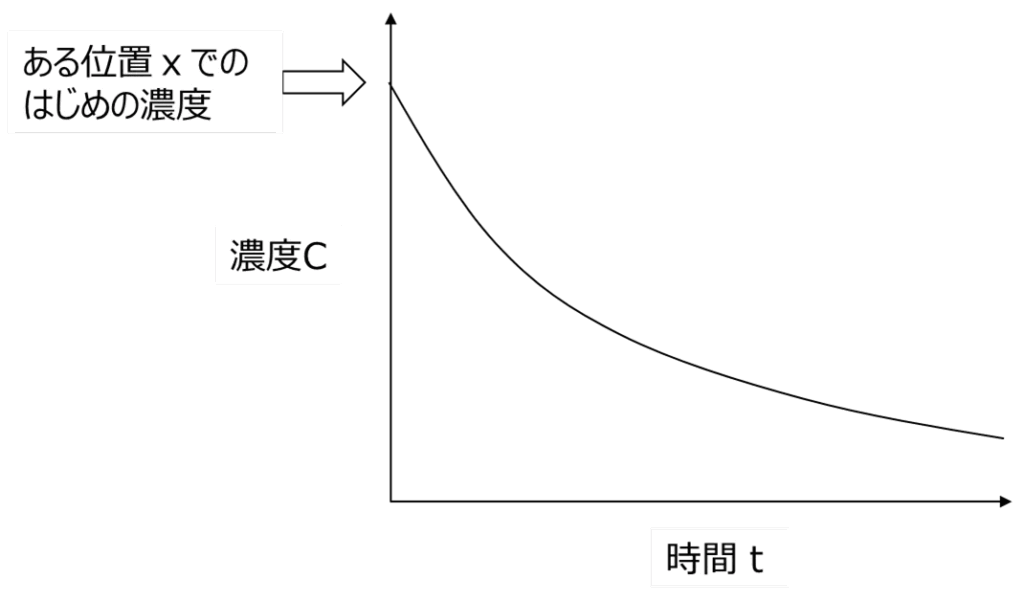
指数関数なので右肩上がりか、右肩下がりのいずれかになりますが、ある位置での物質濃度が時間の経過とともにひたすら右肩上がりになっていくのは現象論的に明らかにおかしいので、右肩下がりになるはずです。
濃度Cが負となるのはおかしいので、まず、Aは正です。その上で指数関数が右肩下がりになるのは、αが負の場合です。
その前提である位置xでの濃度変化を図にすると、次のようになります。指数関数的に減少する、というやつですね。
2. 位置が変わったらどうなるか
「拡散⇒薄まる」という定性的なイメージがつきやすいので、時間の経過とともに濃度が減少するというイメージはスッと入ってくるのではないでしょうか。
問題は、位置が変わったらどうなるか、の方です。
式(10)を改めてみてみると、位置xに関係する部分は
${Bcos(−\frac{D}{\alpha} x)+Csin(−\frac{D}{\alpha} x)}$です。先ほど書いたとおり、これは三角関数の合成によってひとつの三角関数(sinかcos)で表せるので、グラフの雰囲気はこんな感じになります。
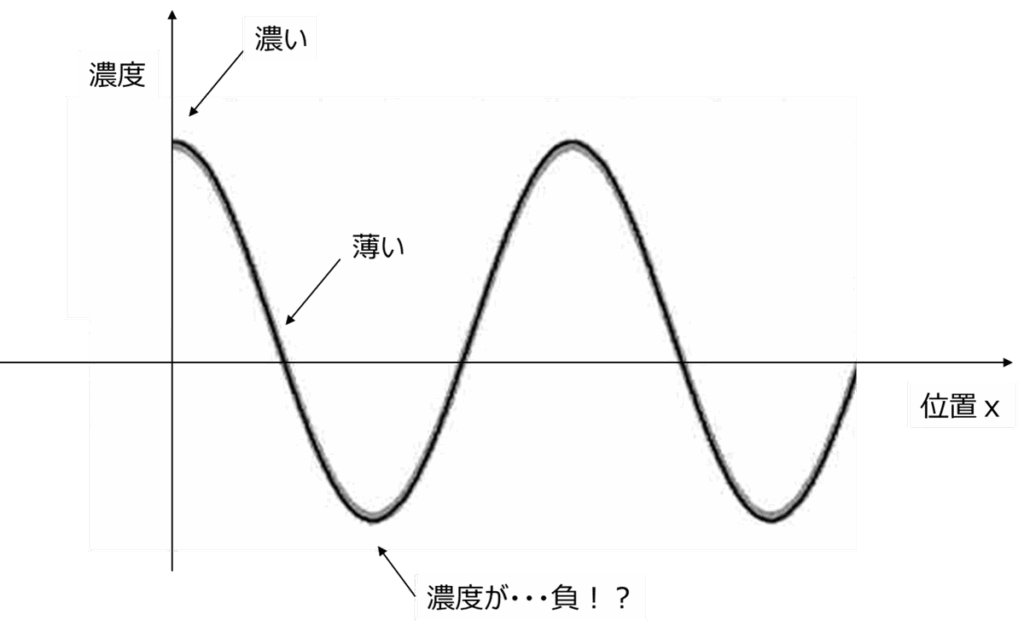
繰り返しますが、これは「濃度分布」です。すると、このグラフのおかしなところがいくつか目に入らないでしょうか。
明らかにおかしなものの1つは、濃度に「負」の領域が存在することです。濃度が負になることは、明らかにあり得ません。たとえば速度など、正負の値を取り得るような物理量であれば問題ないですが、濃度はゼロ以上の値しかとり得ません。
もう1つは、複数の位置xで、濃度のピークが存在することです。たとえばx=0で、排ガスや煙が放たれるとします。その時、x=0に濃度のピークが現れるのは良いとして、そこから離れた位置で同じ濃度ピークが現れるというのは、明らかに実際の現象からかけ離れています。
しかし、次のグラフなら、まだ納得感があるのではないでしょうか。
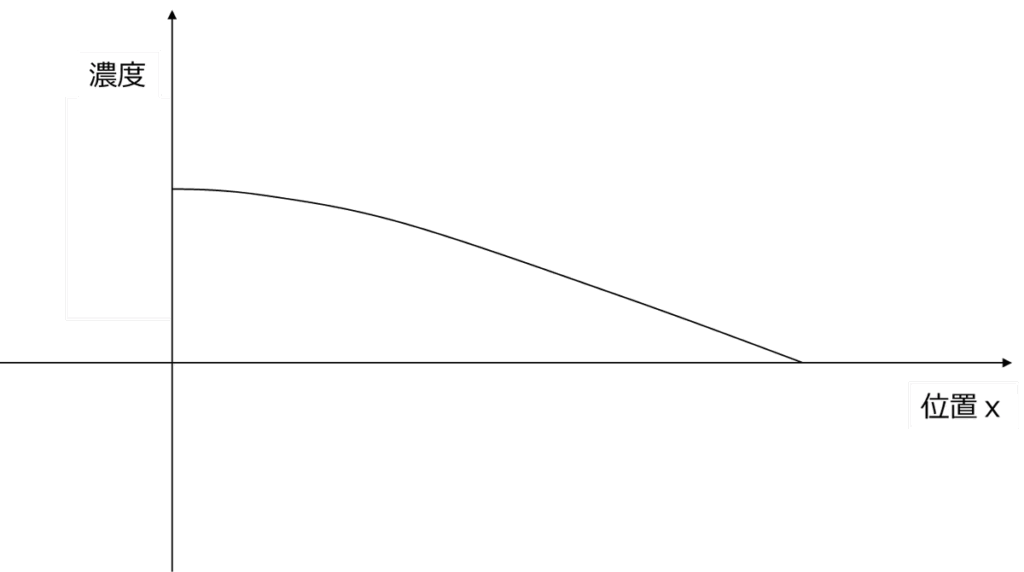
これは、先ほどの三角関数の内、象限をひとつ切り出したものです。これなら、負もないですし、謎の複数濃度ピークの問題も払拭されます。
実際の関数がどうなるかについては、式(10)の定数A, B, Cを決定する必要があり(紛らわしいですが、Dは拡散係数であって、A,B,Cに続く係数とは別です)、初期条件や境界条件といった話に踏み出す必要があります。これらについてはまた別の場で扱うことにします。
まとめ
- フィックの第2法則は「濃度の時間変化=濃度の空間的なカーブの変化」。
- 変数分離で指数関数×三角関数の形に分解できる。
- 拡散の「時間的減衰」と「空間的広がり」を同時に描くことができる。
次回は、実際の大気拡散の予測に使われる「サットンの拡散式」に進みます。
経験則と理論の橋渡しを見ていきましょう。
参考資料
[1] 常微分方程式の解法(大阪大学)
[2] 三角関数の合成のやり方 | 数学 | 苦手解決Q&A | 進研ゼミ高校講座

