富士山の降灰はどう広がるのか？──煙の拡散を支える“数学のしくみ”をのぞく③

ここまで、フィックの第1法則・第2法則を通して拡散現象の基本構造を見てきました。
今回は、それを実際の大気中の煙や排ガスの予測に応用した「サットンの拡散式」を取り上げます。

サットンの拡散式の構成
サットンの拡散式の読み方
まとめ

サットンの拡散式の構成

さて、ここまでは拡散方程式の一般解を眺めてきましたが、これを大気汚染など気象分野に適用できるようあみ出されたものが「サットンの拡散式」で、次のように表されます。

${\frac{C(x,y)}{Q}=\frac{2}{\pi D^2ux^{2−n}}exp{\frac{−r^2}{D^2x^{2−n}}}}$　…式(1)
（参考：An Alignment Chart for Atmospheric Diffusion Calculations）

これは、上記文献の式(2)を引用したもので、それぞれの記号の意味は以下のとおりです（ただし、都合により一部は使用文字を変更しています）。

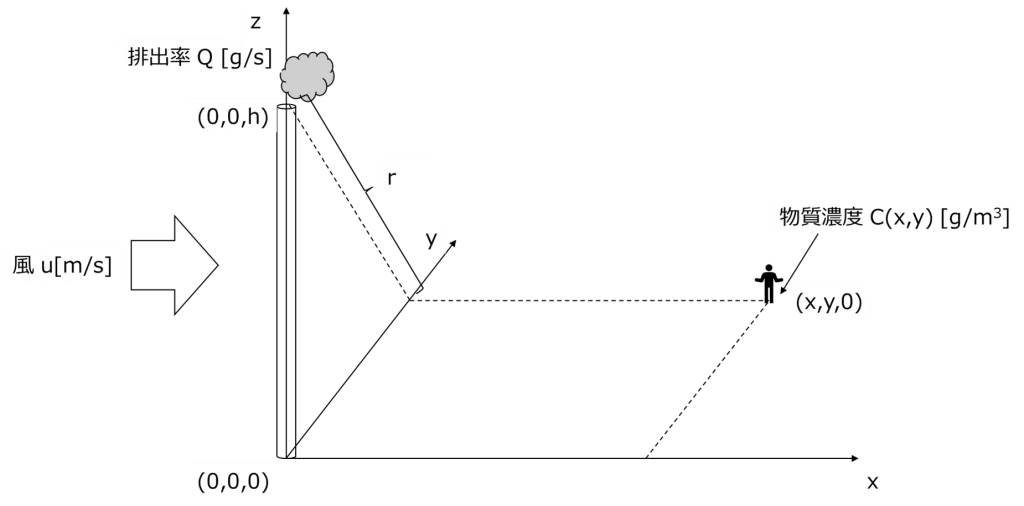
C(x,y) [g/m3]：物質濃度
Q [g/s]：排出率
D2 [mn]：一般化された拡散係数
u [m/s]：平均風速（x軸方向）
x [m]：物質発生源からの水平距離
r [m]：r2=y2+h2
n[-]：安定化パラメータ

これらパラメータと、文献式(2)の座標設定の考え方を図にまとめると下のようになります。(0,0,h)から汚染物質が放出されたとき、地上の位置(x,y,0)における物質濃度を表しているということになります。

前回の記事で登場した式(10)と、今回の式(1)を比べると、形が全然違いますね。あくまで式(10)は拡散方程式の一般解。式(1)は、拡散方程式を元に、現実の事象を記述した具体的な式という位置づけです。

特に、式(10)には登場せず、式(1)で登場する現実的なファクターとして「風速」があります。これが、サットンの拡散式を決定づける特徴です。拡散方程式は純粋な拡散現象のみを記述するものですが、サットンの拡散式では、「風による移流」が考慮されています。

このように、拡散方程式を出発点として、「上空から排出された汚染物質の地表における濃度を計算する」という具体的な目的に即して現実世界のパラメータを取り込んだ式が、サットンの拡散式というわけです。

この式は、拡散方程式の理論に基づきつつ、実測や経験的調整を加えて現実の大気現象にフィットさせたものです。

サットンの拡散式の読み方

さて、式(1)を眺めてみると、色々なことが見えてきます。

①地表の汚染物質濃度が排出率に比例する

左辺の分母となっているQを右辺に移行するとただちに、C(x,y)∝Qの関係が見て取れます。排出率が大きければ大きいほど、地表の汚染物質濃度が高くなります。これは現実的な感覚と整合するでしょう。

②風速uがゼロだと、物質濃度C(x,y)は∞に発散する！？

・・・ような気がしてしまいますが、先ほど書いたように、サットンの拡散式というのは、「風による移流」を前提として記述された式です。なので、風速をゼロにするということ自体がモデルと整合せず、NG行為というわけです。

③nの役割は？？？

当然、サットンは種々の検討の上、式(1)を導いたわけなので、その過程をトレースすれば、自然と安定度パラメータnの意味するところもわかるでしょう。ただ、いまは結果の式を眺めているだけなので、正直、nにどういう効果があるのかは、見えづらいですよね。

そんなときは、グラフ化して、nに色んな値を代入してみて確認するのが手っ取り早いです。ここは、第4回に委ねることにしましょう。

④風下（x軸方向）に行くほど・・・

これも、よくわからん！！右辺のはじめに表れる分数の分母に${x^{2−n}}$とあるので、この部分についてはxが大きくなるほど全体値は小さくなります。

一方、指数関数の${exp{\frac{−r^2}{D^2x^{2−n}}}}$ は、xが大きくなるにつれ増大していきます。xを∞とすると${exp{\frac{-r^2}{D^2x^{2-n}}}→1}$となるので、最終的には${\frac{2}{\pi D^2ux^{2-n}}exp\frac{-r^2}{D^2x^{2-n}}}$全体としてはxの増加に伴って減少することが予想されますが、これについても、グラフ化してハッキリさせるのが良いでしょう。