富士山の降灰はどう広がるのか？──煙の拡散を支える“数学のしくみ”をのぞく④

さて、本シリーズ最後となる第４回目はお待ちかね、「グラフ化」です。ここでは、プログラミング言語のPythonを使ってサットンの拡散式の描画を試みます。

高校数学でも、微分の単元で、ある程度関数のグラフ化を扱います。しかし、残念ながら、初等数学で描けるグラフの種類には限界があります。プログラミングを使えば、初等数学では難しい描画も難なく可視化できます。そして、プログラミングを使って可視化するスキルを身に着けておくことで、関数への理解がより深まることが期待されます。

Pythonで描くサットンの拡散式

では、サットン式や拡散式を実際に描いてみるとどうなるでしょうか？以下が、Pythonスクリプトです。

import numpy as np # numpyという数値計算ライブラリをnpという名前でインポートする
import matplotlib.pyplot as plt # matplotlibというライブラリのなかのpyplotというモジュールをpltという名前でインポートする

# --- 1. サットン拡散式の定義 ---
def sutton_diffusion_concentration(x, y, h, Q, D_squared, u, n):
    """
    サットンの拡散式に基づく濃度 C(x,y) を計算する。

    パラメータ:
    x (float or array): 物質発生源からの水平距離 [m]
    y (float or array): 横風距離 [m]
    h (float): 物質発生源の高さ [m]
    Q (float): 排出率 [g/s]
    D_squared (float): 一般化された拡散係数 D^2 [m^n]
    u (float): 平均風速 [m/s]
    n (float): 安定化パラメータ [-]
    
    戻り値:
    C (float or array): 物質濃度 [g/m3]
    """
    
    # r^2 の計算: r^2 = y^2 + h^2
    r_squared = y**2 + h**2
    
    # 分母の x^(2-n) の項
    x_term = x**(2 - n)
    
    # 濃度 C/Q の計算
    C_over_Q = (2 / (np.pi * D_squared * u * x_term)) * np.exp(-r_squared / (D_squared * x_term))
    
    # 濃度 C の計算 (C = C/Q * Q)
    C = C_over_Q * Q
    
    return C

# --- 2. パラメーター設定 (仮定値) ---
# 典型的な安定度 n=0.25 (弱不安定〜中立) を仮定
Q = 1.0       # 排出率 [g/s]
h = 10.0      # 排出源の高さ [m]
u = 5.0       # 平均風速 [m/s]
n = 0.9      # 安定化パラメータ [-] (0 < n < 1)
D_squared = 0.1  # 一般化された拡散係数 D^2 [m^n] (n=0.25なので m^0.25)

# --- 3. グラフ描画 ---

## 3.1. 風下距離 (x) による濃度変化 (y=0, z=0: 地表中心軸上)
x_values_downwind = np.linspace(10, 1000, 500) # x = 10m から 1000m まで
y_centerline = 0.0 # y = 0m

C_downwind = sutton_diffusion_concentration(
    x=x_values_downwind,
    y=y_centerline,
    h=h,
    Q=Q,
    D_squared=D_squared,
    u=u,
    n=n
)

#図の作成；新しい描画キャンバス（図）を作成し、サイズを幅10インチ、高さ5インチに設定。
plt.figure(figsize=(10, 5)) 

#線グラフの描画；x_values_downwind をX軸、C_downwind * 1e6 (濃度を[g/m^3] から [µg/m^3] に変換したもの) をY軸として、線グラフを描画
plt.plot(x_values_downwind, C_downwind * 1e6, label=f'h={h}m, n={n}', color='darkred') 

#グラフタイトルの設定；グラフの上部タイトルを「Concentration C vs. Downwind Distance x (Ground, Centerline)」に設定
plt.title('Concentration C vs. Downwind Distance x (Ground, Centerline)')

# X軸ラベルの設定；X軸（横軸）に「Downwind Distance x[m]$」というラベルを設定
plt.xlabel('Downwind Distance x [m]')

# Y軸ラベルの設定；Y軸（縦軸）に「Ground Concentration C[µg/m^3]」というラベルを設定
plt.ylabel('Ground Concentration C [µg/m³]') 

# グリッド線の表示；グラフ内に格子線（グリッド）を表示し、線のスタイルを破線 (--)、透明度を0.6に設定
plt.grid(True, linestyle='--', alpha=0.6)

# 凡例（レジェンド）の表示；label で設定した情報（この場合は $\text{h}$ や $\text{n}$ の値）を含む凡例ボックスをグラフ上に表示
plt.legend()

# レイアウトの調整；ラベルやタイトルが図の枠外にはみ出さないよう、グラフ全体のレイアウトを自動で調整
plt.tight_layout()

# グラフの表示；作成した図（Figure）を画面に表示
plt.show()

## 3.2. 横風距離 (y) による濃度変化 (特定 x での断面)
x_slice = 200.0  # x = 200m 地点での断面をプロット
y_values_crosswind = np.linspace(-50, 50, 500) # y = -50m から 50m まで

C_crosswind = sutton_diffusion_concentration(
    x=x_slice,
    y=y_values_crosswind,
    h=h,
    Q=Q,
    D_squared=D_squared,
    u=u,
    n=n
)

plt.figure(figsize=(10, 5))
plt.plot(y_values_crosswind, C_crosswind * 1e6, label=f'x={x_slice}m, h={h}m', color='navy')
plt.title(f'Concentration C vs. Crosswind Distance y (at x = {x_slice}m)')
plt.xlabel('Crosswind Distance y [m]')
plt.ylabel('Ground Concentration C [µg/m³]') # g/m3 を µg/m3 に変換
plt.grid(True, linestyle='--', alpha=0.6)
plt.legend()
plt.tight_layout()
plt.show()

スクリプトの読み方

先ほどの白文字だけだと、プログラミング言語初見者にはちょっと（だいぶ？）読みづらいかと思います。そこで、上のスクリプトを丸っとコピーして、たとえばNotepad++のようなメモ帳ソフトに貼り付け、「Sutton_equation.py」という名前で保存してみてください。

すると、以下のようにカラフルなスクリプトに変身するかと思います。

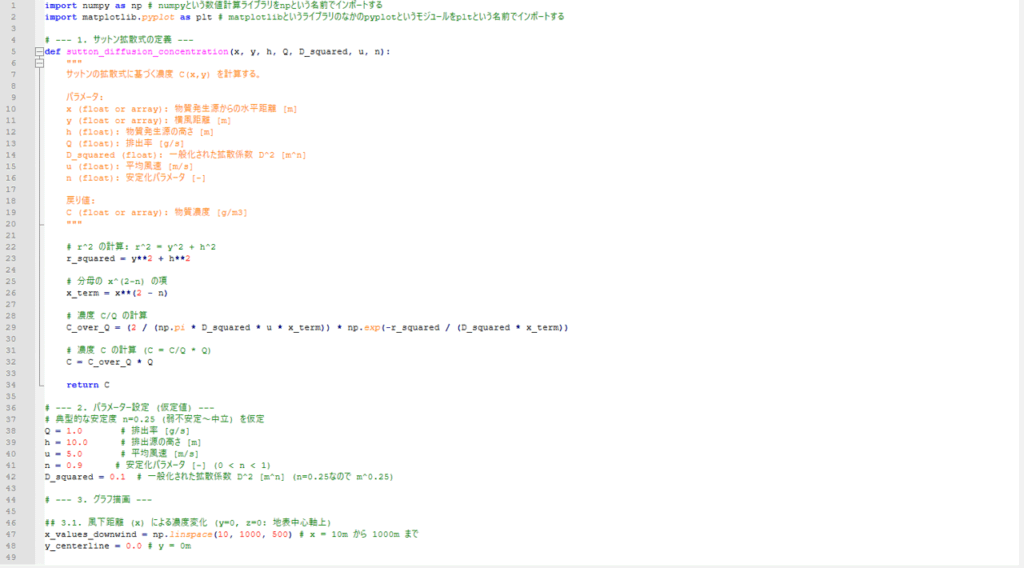
コメントアウト

まず、「#」から始まる緑文字の部分は、「コメントアウト」と呼ばれるもので、いわば「注釈」です。ここに書いてあることは、あくまでスクリプト本体の説明書きに過ぎないので、プログラムとして実行されることはありません。

Docstring

また、「”””」で囲われたオレンジの部分は「Docstring（ドクストリング）」というもので、以下のような箇所に設けられます。

• モジュール（ファイル全体）の先頭
• クラスの定義直後
• 関数（メソッド）の定義直後

今回の場合は、「関数の定義直後」に挿入されており、その関数が何をするのか、どのような引数（パラメータ）を取るのか、何を返すのかを説明しています。

Docstringの最も重要な特徴は、「実行時にアクセスできる」という点で、 Pythonの対話型インタープリタやJupyter Notebookなどで help() 関数を使うと、このDocstringの内容が表示されます（例：help(sutton_diffusion_concentration)と打つと、sutton_diffusion_concentration関数が何をする関数なのか説明してくれる）。

いずれにせよ、コメントアウトと同様、Docstringもプログラムとして実行されることはありません。 つまり、これら緑文字、オレンジ文字を除いた部分のスクリプトが実際には実行されていくわけですが、それぞれの行で何が実行されるのかについてはコメントアウトにくどくどと説明書きしているので、それを読んでいただければ追っていけるはずです。是非、トライしてみてください。

スクリプトの実行

このスクリプトは、以下の手順で実行できます。

①「Sutton_equation.py」をPC内のどこかに保存する
②その「どこか」を図2の青ハイライト部の要領でコピーする
③デスクトップ下方の検索バーで「cmd」と入力し、「コマントプロンプト」を立ち上げる
④コマンドプロンプトで「cd 2でコピーした文字列」と入力し、Enterキーで実行する⑤Suttons_equation.pyと入力し、実行する（図3参照）

※上記の説明は、Windows11を前提としています
※Python3系がインストールされていることを前提としています

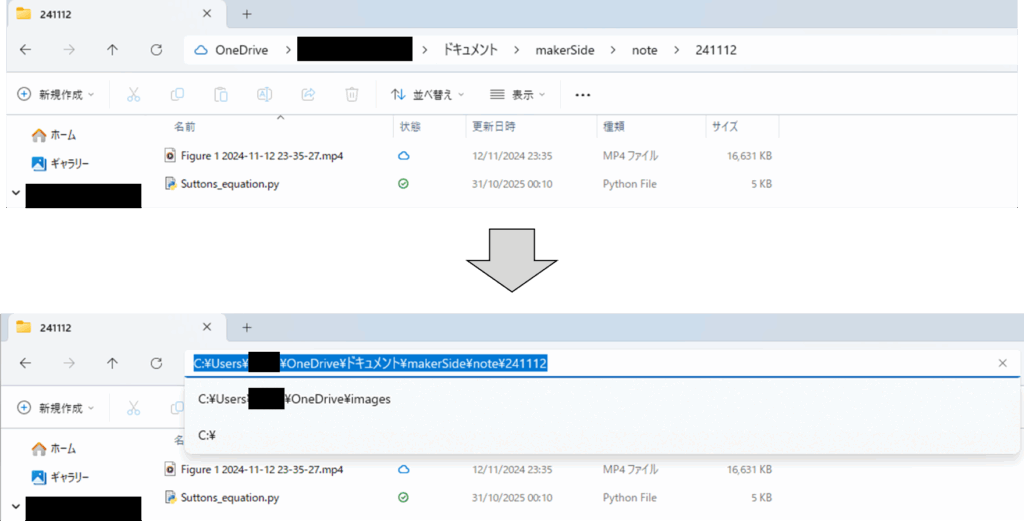
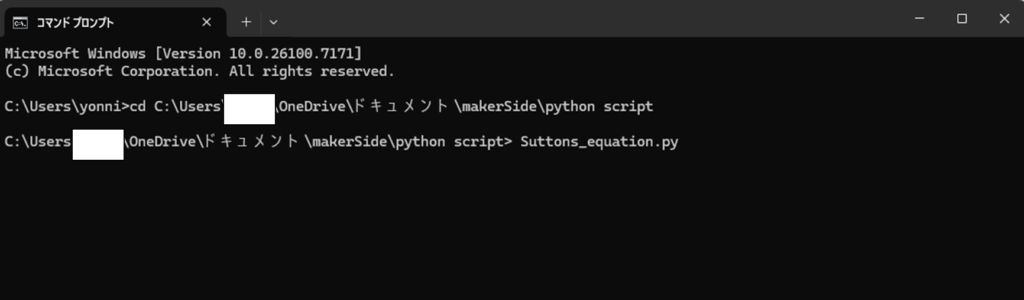
以上を実行すると、図4のようなグラフが表示されるはずです。

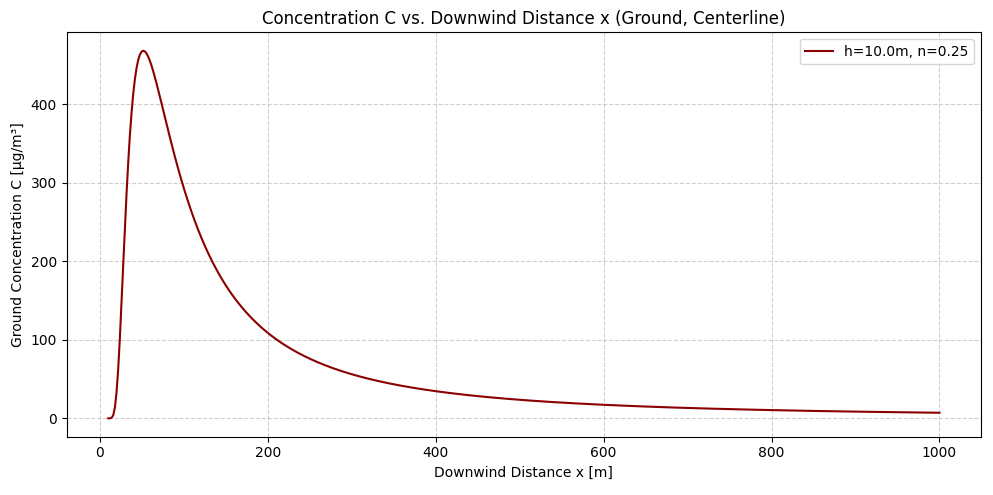
図4は横軸を風下方向（x軸方向）にとっており、縦軸が地表（y=0, z=0）における物質濃度をμg/m3で表したものです。排出源の高さはh=10m、安定度パラメータはn=0.25と設定しています。図4は、排出源から数十メートル風下方向に離れた位置で物質濃度がピークを取り、それ以降は減少していく様子を表しています。

これでまず、前回記事の④の疑問に答えたことになります。つまり、xが増加すると、あるところまでは濃度が増大するものの、ピークを取って以降は減少に転じるということです。

もう一つ、前回記事の③の疑問に答えるために、今度は安定度パラメータをn=0.9と設定してみましょう。すると、全く違う様相が現れることが図5から確認できます。

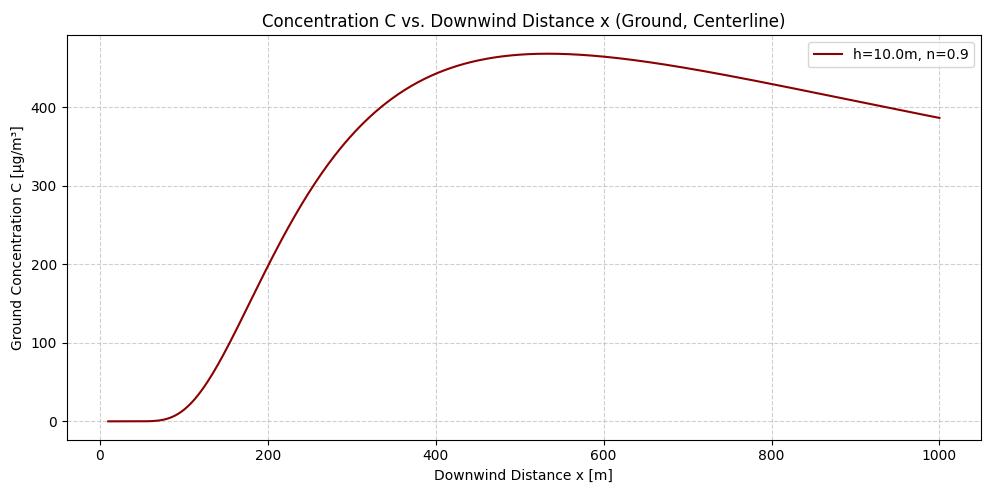
安定度パラメータnというのは、大気の安定度を表しているものです。nの値が大きいほど安定、小さいほど不安定であることを表します。

nの値が小さい図4ではx<100mの領域で地表濃度ピークを迎え、nの値が大きい図5ではx=500mくらいでようやく地表濃度ピークを迎えます。これはつまり、nが小さく大気が不安定な場合は上空で放出されたガスが早々に拡散するのに対し、nが大きく大気が安定している場合はなかなか拡散しないということを反映した結果と解釈できます。

おわりに

さて、「大気中の煙の広がり」を足掛かりに、フィックの法則に表れる常微分方程式、そこから導かれたサットンの拡散式について、その読み方について扱ってきました。また、Pythonを使って、サットンの拡散式の描く煙の広がり方の可視化を試みました。 中高、大学の数学は解くことに主眼がおかれがちですが、数式を「読む」スキルを身に着けることによって、日常をより深く味わう手段が増えることと信じています。