「EV vs ガソリン車、どっちがお得？」数学的にガチ比較してみた結果

最近また、EVに関するニュースをよく耳にするようになりました。満を持してEVの購入を視野に入れて検討されている人も多いのではないでしょうか。

EV（電気自動車）とガソリン車、どちらの方が長期的にお得なのでしょうか？ それを比較したサイトは色々ありますが、細かい条件設定にまで踏み込んでガチ議論したものは知る限り見当たりません。

そこで、「EVとガソリン車のどちらがお買い得か」をテーマに、数学的に突っ込んだ議論をしてみましょう。

車の所有にかかるコストの構成

まず車を保有することの経済性を比較する上で、車の所有にかかる費用がざっくり、「初期費用」と「維持費」の2つで構成されているという点を押さえる必要があります。

購入時にかかるのは購入費用、維持するのにかかるのは自動車税と、電気または燃料費です。リペア代や細々としたアクセサリ費などは検討対象外とします。あとでパラメータを振った検討をしますが、いったん下表のパラメータで計算を進めることにします。

項目	記号	数値	単位
EVの購入費用	${M_{cap,ev}}$	400	万円
ガソリン車の購入費用	${M_{cap,gas}}$	250	万円
EVの自動車税	${M_{opt,ev}}$	25,000	万円/年
ガソリン車の自動車税	${M_{opt,gas}}$	36,000	万円/年
EVの電費	${l_{ev}}$	7	km/kWh
ガソリン車の燃費	${l_{gas}}$	15	km/L
年間走行距離	${L}$	4,344	km
電気料金	${m_{ev}}$	31	円/kWh
ガソリン料金	${m_{gas}}$	174.5	円/L

車をN年間保有した場合のEVとガソリン車のコスト比較

一般に、同程度の車種であれば、ガソリン車よりもEVの方が購入費用が高くつきます。

もし維持費までEVの方が高ければ、単にコスト比較をした場合、あっさりとガソリン車に軍配が上がってしまいます。EVの方が維持費が安ければ、ある程度の年数保有していれば、トータルでガソリン車よりもお得になる瞬間が訪れるかもしれません。

そのような検討をしたいがために、車の保有年数をN年とおいた上で、N年間での累積コストの比較をしていきます。

EV、ガソリン車をN年間保有した場合のトータルコストを文字で書くと、次のような感じです。

EVをN年間保有した場合の総費用＝EV購入費用＋N年分の自動車税＋N年分の電気代
ガソリン車をN年間保有した場合の総費用＝ガソリン車購入費用＋N年分の自動車税＋N年分のガソリン代

この内、購入費用は冒頭の表のとおりですし、自動車税も、冒頭の表の値にNを掛けるだけで単純なので、「電気代」と「ガソリン代」をどう考えるかについて、少し丁寧にみていくことにします。

EVの年間電気代

EVの年間電気代は、電気料金[円/kWh]に、年間で使用した電力量[kWh]を掛けることで求められます。分数の計算と同じように、単位同士も、「円/kWh x kWh = 円」のように計算することができます。

電気料金は電力会社側で決めることなので、考えるところではありません。今回の場合は、表に書いてある数字のとおりです。

年間電力消費量をどう計算するかですが、これも先ほどの単位計算の応用です。年間走行距離[km]と電費[km/kWh]がわかれば、「km÷km/kWh＝kWh」という風に、電力消費量の単位を導くことができます。これが、年間電力消費量にあたるわけです。

なので、EVの年間電気代を${M_{opf,ev}}$、年間電力消費量を${F_{ev}}$とすると

${M_{opf,ev}=m_{ev} \times F_{ev}=m_{ev} \times \frac{L}{l_{ev}}=31 \times \frac{4344}{7}=19,237}$[円]となります。

ガソリン車の年間ガソリン代

ガソリン車の年間ガソリン代は、ガソリン料金[円/L]に、年間で使用したガソリン消費量[L]を掛けることで求められます。

年間ガソリン消費量をどう計算するかですが、先ほどと同じノリで、年間走行距離[km]と燃費[km/L]がわかれば、「km÷km/L＝L」という風に、ガソリン消費量の単位を導くことができるので

${M_{opf,gas}=m_{gas} \times F_{gas}=m_{gas} \times \frac{L}{l_{gas}}=174.5 \times \frac{4344}{15}=50,535}$[円]となります。

EVをN年間保有した場合の総費用の計算

EVをN年間保有した場合の総費用＝EV購入費用＋N年分の自動車税＋N年分の電気代

というわけで、上の式にしたがってEVをN年間保有した場合の総費用を計算してみると、次のようになります。

${M_{ev,N}=M_{cap,ev}+N.M_{opt,ev}+N.M_{opf,ev}}$

${=400+2.5N+1.9237N=400+4.4237N}$[万円]となります。数字がデカくなるので、単位は[万円]としておきました。

EVをN年間保有した場合の総費用は、Nに関する1次式の形で表されたことになります。

ガソリン車をN年間保有した場合の総費用の計算

ガソリン車をN年間保有した場合の総費用＝ガソリン車購入費用＋N年分の自動車税＋N年分のガソリン代

上の式にしたがってガソリン車をN年間保有した場合の総費用を計算してみると、次のようになります。

${M_{gas,N}=M_{cap,gas}+N.M_{opt,gas}+N.M_{opf,gas}}$

${=250+3.6N+5.0535N=250+8.6535N}$[万円]となります。

ガソリン車をN年間保有した場合の総費用も同様に、Nに関する1次式の形で表されたことになります。

何年目までEV／ガソリン車がお得か、1次不等式で評価する

これで、EVもガソリン車もそれぞれ、N年目まで保有した場合の総費用がNに関する1次関数で表されたことになるので、あとは単純にその大小を比較してあげましょう。

「EVをN年間保有した場合の総費用 < ガソリン車をN年間保有した場合の総費用」となるようなNを求める、ということになります。

${400+4.4237N<250+8.6535N \Leftrightarrow 150 < 4.2998N \Leftrightarrow 34.885… < N }$

この結果をどう翻訳するかというと

「Nが34.885…年より大きくないと、EVを保有した場合の総費用がガソリン車を保有した場合の総費用を下回ることはない」

ということです。実質的に、EVの総費用がガソリン車の総費用を下回ることはない、と言っているということです。

パラメータ変動の影響を織り込んでみよう

変動するパラメータはどれか？

いまの結果は、冒頭の表に決め打ちしたパラメータの値をそのまま使って計算を進めていった結果です。でも実際は、変動するパラメータ、ありますよね？

「EVの購入費用」「ガソリン車の購入費用」「EVの電費」「ガソリン車の燃費」「年間走行距離」「電気料金」「ガソリン料金」なんていうのは、もっと違う数字の可能性が十分にあり得ます。

そこで、これらは文字のまま残したまま、「EVをN年間保有した場合の総費用 < ガソリン車をN年間保有した場合の総費用」の式を書き下してみることにしましょう。

${M_{ev,N}<M_{gas,N}}$

${\Leftrightarrow M_{cap,ev}+N.M_{opt,ev}+N.M_{opf,ev} < M_{cap,gas}+N.M_{opt,gas}+N.M_{opf,gas}}$

${\Leftrightarrow M_{cap,ev}+2.5N+N.M_{opf,ev} < M_{cap,gas}+3.6N+N.M_{opf,gas}}$

ここでいったん式変形をストップさせておきましょう。

文字がいっぱい不定のまま残っています。さて、ここからどういう風に持っていきましょう。

パラメータに制約をかけて不等式を追い込んでいく

先ほどの「決め打ち」の計算では、Nは34年超えというぶっ飛んだ結果が出てきました。Nというのは、いま保有年数として設定しているわけですから、ぶっ飛んだ、というのは、平均的な保有年数よりはるかに大きいという意味です。

2023年3月時点での自動車の平均使用年数は、13.42年だそうです。

そこで、ここからは発想を逆転させて、「Nを求める」のではなく、逆に「Nに制約をかける」ことで、他のパラメータがどう影響を受けるのか見ていくことにします。

具体的には、Nが13.42年以下という条件をつけた場合に、他のパラメータの制約がどうなってくるのか、を見たいと思います。

${\Leftrightarrow M_{cap,ev}- M_{cap,gas}<N.M_{opf,gas}-N.M_{opf,ev}+1.1N}$

${\Leftrightarrow \frac{M_{cap,ev}- M_{cap,gas}}{M_{opf,gas}-M_{opf,ev}+1.1}<N=13.42}$

${\Leftrightarrow \frac{M_{cap,ev}- M_{cap,gas}}{\frac{m_{gas}}{10000} \times \frac{L}{l_{gas}}-\frac{m_{ev}}{10000} \times \frac{L}{l_{ev}}+1.1}<13.42}$

${m_{gas},m_{ev}}$をそれぞれ10,000で割っているのは、単位を[万円]に統一するためです。この式を満足するような${M_{cap,ev}, M_{cap,gas}, m_{gas}, m_{ev}, L, l_{gas}, l_{ev}}$の組み合わせがあれば、保有年数の13.42年以内に、EVがガソリン車よりもお買い得になる可能性があるということです。

文字が多いときは、ターゲットを見失わないことが大事！

これでもまだ左辺には7つもの不定数が残っているわけですが、最終的には「EV車を購入するかどうかの意思決定をしたい」ということを考えると、不等式の解が最終的に、EV車の購入費用に関して何らかの示唆を与える方がいいような気がします。つまり、分子は文字のまま残しておいた方がよいでしょう。

というわけで、分母のパラメータに縛りをかけることにします。

分数全体で上限が決まっているので、分子を最大化するということは分母も最大化するということ、逆に、分子を最小化するということは分母も最小化するということです。

分母が最大となるのは、${m_{gas}}$が最大、${l_{gas}}$が最小、${m_{ev}}$が最小、${l_{ev}}$が最大となった場合

分母が最小となるのは、${m_{gas}}$が最小、${l_{gas}}$が最大、${m_{ev}}$が最大、${l_{ev}}$が最小となった場合です。

電気料金とガソリン料金は市場状況や政策によって変動しますが、だいたい次のようなレンジで動いています。

• 電気料金（${m_{ev}}$）： 20円/kWhから40円/kWh​
• ガソリン料金（${m_{gas}}$）： 150円/Lから200円/L​

${l_{gas}}$、${l_{ev}}$はそれぞれ燃費、電費で、平坦な道を走ったり坂を登ったりで時々刻々と値の変わるパラメータではありますが、かといって電気料金やガソリン料金のようにあるレンジを想定することもナンセンスなので、ここは冒頭の表のとおり、それぞれ平均的な代表値として${l_{gas}=15}$、${l_{ev}=7}$を想定しましょう。

あとは、年間走行距離${L}$だけです。ここは、場合分けしましょう。

１）年間走行距離が5,000kmの場合

${\frac{M_{cap,ev}- M_{cap,gas}}{\frac{m_{gas}}{10000} \times \frac{L}{l_{gas}}-\frac{m_{ev}}{10000} \times \frac{L}{l_{ev}}+1.1}<13.42}$

${\Leftrightarrow \frac{M_{cap,ev}- M_{cap,gas}}{\frac{m_{gas}}{10000} \times \frac{5000}{15}-\frac{m_{ev}}{10000} \times \frac{5000}{7}+1.1}<13.42}$

${\Leftrightarrow M_{cap,ev}- M_{cap,gas}<13.42\times (\frac{m_{gas}}{10000} \times \frac{5000}{15}-\frac{m_{ev}}{10000} \times \frac{5000}{7}+1.1)}$

ごちゃごちゃしているように感じられるかもしれませんが、先ほど書いたように、この不等式のゴールは「EV車の購入費用に関して何らかの示唆を得ること」です。つまり、${M_{cap,ev}}$にどういう制約がつくのかを知りたいのです。

右辺がごちゃごちゃしてるように見えますが、これは${m_{gas}}$と${m_{ev}}$の2変数についての1次式です。

右辺をまるっとｚとおき、${z=13.42\times (\frac{m_{gas}}{10000} \times \frac{5000}{15}-\frac{m_{ev}}{10000} \times \frac{5000}{7}+1.1)}$を大真面目にmgas, mev, z座標空間にプロットすると、次のような図になります。

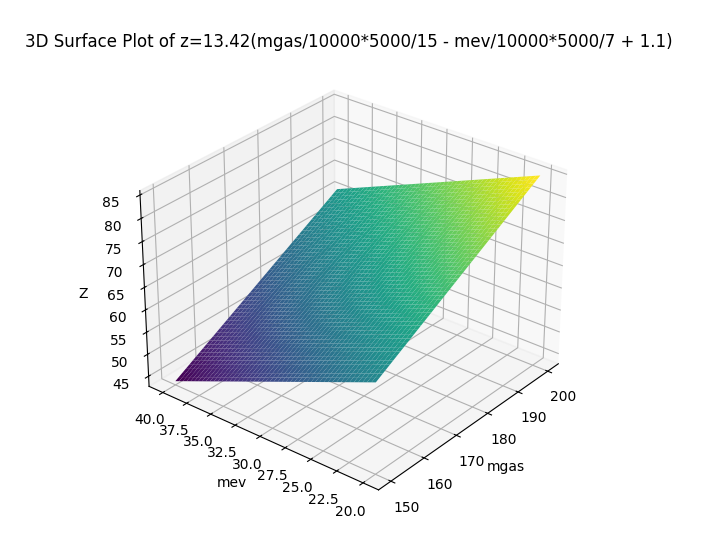
ガソリン料金mgasが高いほど、電気料金mevが安いほどzが高くなることがわかるかと思います。zが高くなるということは、左辺の${M_{cap,ev}- M_{cap,gas}}$も併せて大きくなる、つまりEVとガソリン車の値差が許容される側に振れるということになります。ガソリン料金mgasが高くて、電気料金mevが安い方がEVにとっては有利だということで、定性的な解釈と一致しますね。

この図から、右辺の値は43.5～85.0の間で振れることがわかります。つまり、${m_{gas}}$と${m_{ev}}$の値の組み合わせによって

${M_{cap,ev}- M_{cap,gas}<43.5}$から
${M_{cap,ev}- M_{cap,gas}<85.0}$までのケースがあるということです。

この結果は何を物語っているのでしょうか。

この一連の不等式の出発点は「EVをN年間保有した場合の総費用 < ガソリン車をN年間保有した場合の総費用」でした。それを変形していってたどり着いた先が、先ほどの${M_{cap,ev}, M_{cap,gas}}$についての式です。

つまり、「年間走行距離が5000km程度の場合で、13.42年乗りつぶすことを前提にすれば、ガソリン料金${m_{gas}}$と電気料金${m_{ev}}$がどんなに振れたとしても、EV車がガソリン車より85万以上高いようならペイしない（元が取れない）」というのが結論です。

２）年間走行距離が10,000kmの場合

年間走行距離5,000kmというのは控えめな数字なので、もう1パターン、年間走行距離が10,000kmの場合はどうか、結果を示しておきましょう。

考え方は先ほどと全く同じです。ただ、5,000を10,000に置き換えればいいので

${M_{cap,ev}- M_{cap,gas}<13.42\times (\frac{m_{gas}}{10000} \times \frac{10000}{15}-\frac{m_{ev}}{10000} \times \frac{10000}{7}+1.1)}$

${m_{gas}}$と${m_{ev}}$の値の組み合わせによって

${M_{cap,ev}- M_{cap,gas}<72.2}$から
${M_{cap,ev}- M_{cap,gas}<153}$までのケースがあります。

この解釈は

「年間走行距離が10000km程度の場合、13.42年乗りつぶすことを前提にすれば、ガソリン料金${m_{gas}}$と電気料金${m_{ev}}$の組み合わせ次第では、EV車がガソリン車より152万円程度高くてもペイする（元が取れる）」となります。

要は、年間走行距離が大きい方が、EVの購入費用が多少高くても元が取れる可能性があるということになります。

ちょっと長くなってしまいましたが、文字が多くて一見ごちゃごちゃしく見える不等式でも、「EV車の購入費用に関して何らかの示唆を得たいから、${M_{cap,ev}}$にどういう制約がつくのかを知りたい」というゴールを見失わずにいれば、他のパラメータに対してどういう制約をかけたり、値を仮定したりすればいいかという動きが見えてくるのです。

まとめ

「EVとガソリン車のコスト比較」をケーススタディとして、購入の意思決定をするための数学的手法、特に1次不等式の解釈の仕方について扱いました。

この記事では、車両保有年数を最終的に（ネットで調べた）13.42年という値決め打ちで進めていきましたが、これがたとえば「10年」や「15年」だったら結果にどう影響するのか考えてみるのも、また一興かもしれませんね。

また、この記事では、たしかに一見、ガソリン料金、電気料金の変動を織り込んでいるように見えるのですが、実は車の保有期間は一定値とする（たとえば、ガソリン料金が200円/Lなら13.42年間は200円/Lのまま）ことを暗に仮定しています。実際の年々の料金変動が結果にどう影響するかを考えてみるのもまた、面白いかもしれませんね。