電池の内部抵抗が増加して電池性能が劣化するってどゆこと？

こちらの記事で、鉛充電池の「内部抵抗が増加して電池性能が劣化する」としれっと書きました。

わかったようなわかんないような、な感じしませんか？

内部抵抗というのが、文字通り電池内部の抵抗で、電解液の消耗・蒸発や酸化・不純物の蓄積による電極の劣化、セパレーター（絶縁膜）の劣化で生じるものだということは前回の記事で書きました。

ただ、「内部抵抗が増加したら、具体的にどんな悪いことがあるの？」という疑問には答えていません。

今回は、そんな疑問について補足したいと思います。

起電力と端子電圧の違いを押さえよう

「そもそも電池の性能が劣化するって、具体的にどんな悪いことがあるの？」

この疑問に答えるためには、まず電池には起電力と端子電圧というものがあるということを知っておく必要があります。

言ってみれば、起電力は電池が出せる電圧のポテンシャル、端子電圧は実際に電池が出す電圧のパフォーマンスです。

起電力は理論上計算されるポテンシャル

起電力とは、「電池内部の化学反応によって発生する理論上の電圧」で、「電極材料と電解液の組み合わせ」によって決まります。

たとえば、その辺で買ってきた単３のマンガン乾電池の電圧が1.5Vだというのは皆さんよく知っています。ここで言っている1.5Vというのが、起電力です。この1.5Vというのが「電池内部の化学反応によって発生する理論上の電圧」ということですが、具体的には、標準電極電位の差として計算されます。

化学の授業をざっくり記憶されている方なら、「なんかの溶液に金属の電極を２つ突っ込んだら電池ができる」ということをなんとなく覚えているのではないでしょうか。

電池ができる、ということは、電流が流れる、つまり電子の移動が起きるということです。電子の移動が起きるということは見方を変えると、そこに電圧が発生しているということです。電圧というのは、電位と電位の差、つまり電位差です。

では、「なんかの溶液に金属の電極を２つ突っ込んだ」ときの電圧は、何と何の電位の差なのか？ということですが、それが、２つの電極に生じる電位の差ということなのです。この時に計算に使う電位が、標準電極電位です。

たとえばマンガン乾電池は、負極と正極でそれぞれ以下の酸化還元反応が起きますが、亜鉛（Zn）の標準酸化電位が$${E^0=-0.76}$$[V]、マンガン酸化物（MnO₂）の標準還元電位が$${E^0=0.74}$$[V]ということで、この差分として1.5Vが計算されます。

• 負極（酸化）：$${Z_n→Zn^{2+}+2e^−}$$
• 正極（還元）：$${2M_nO_2​+2e^−+2NH_4+​→Mn_2​O_3​+2NH_3​+H_2​O}$$

この標準電極電位は、標準水素電極を基準（0V）とした時の電位で、＋だと水素より電子を受け取りやすい（還元されやすい）、ーだと水素より電子を出しやすい（酸化されやすい）ことを意味します。標準水素電極というのは、水素ガス（H₂）の電極反応を基準にした電極です。

まとめると、電極材料と電解溶液が決まった時点で、標準電極電位が決まるので、電池がどれだけの起電力を生じるかも決まるのです。

実際に電池から取り出せる電圧は「端子電圧」

では、たとえば起電力1.5Vの電池があったとして、その電池からまるっと1.5Vの恩恵に授かることができるかというと、答えは「ノー」です。

ここからは化学というよりはちょっとした物理の話になります。次の図を見てください。

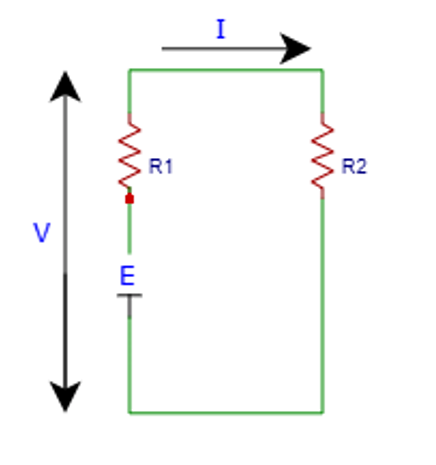
この図でいうEが起電力で、これがいま1.5Vです。電池を何らかの機器に接続して使うわけですが、その機器の抵抗をいま、まるっとR2として表してます。

こうして電池を外部の機器に接続すると電流Ｉが流れるわけですが、その時に、電池の内部抵抗Ｒ１が問題になってきます。電池単体では電流は流れないので、内部抵抗があっても何も起こりません。ところが、電流が流れることによって、この内部抵抗で電圧降下が起きます。

実際に電池から取り出せる電圧というのは、この内部抵抗での電圧降下を加味した電圧で、これを端子電圧と呼んでいます。図で言うVですね。こうして、起電力と端子電圧とに差が生じるのです。

仮に内部抵抗をR1=0.5Ω、機器の抵抗をR2=2Ωとします。この単なる直列回路では、R1とR2に流れる電流が同じなので、R1とR2で起こる電圧降下は、それぞれの抵抗に比例します。なので、実際にR2に与えられる電圧（R2にかかる電圧）は$${V=1.5 \times \frac{2}{0.5+2}=1.2[V]}$$になります。1.5Vはかからないわけですね。

まとめ

というわけで、結論はシンプルです。