お子さんが中学校に入って数学を学ぶとき、もしかしたら親御さん自身が学生の頃に感じた疑問を、またお子さんも感じるかもしれません。
「円柱とか円錐とか、こんな立体図形の体積や表面積の計算… これ、社会に出てから使う機会あるの?」
正直、当時の私もテストのために公式を一生懸命覚えたものの、その「使い道」まではピンと来ていませんでした。
たしかに、全ての人が日常生活で直接的にこれらの公式を使うわけではないかもしれません。でも、実は私たちの身の回りにあるたくさんのもの、そして将来お子さんたちが関わるであろう様々なテクノロジーは、この空間図形の知識なしには成り立たないんです!
今回は、中学で学ぶ空間図形が、一体社会のどこで、どんな風に役立っているのかを一緒に探検してみましょう。これは、お子さんの「なぜ学ぶの?」という疑問に答えるヒントにも、親御さん自身の「なるほど!」という発見にも繋がるはずです。
中学で習った空間図形、ちょっと思い出してみよう!
まずは、中学校でどんな立体図形を習ったか、簡単におさらいです。
例えば、トイレットペーパーの芯やジュースの缶のような「円柱」、ビルのような「角柱」。これらは「柱体」の仲間です。アイスクリームのコーンや、お城の屋根のような「円錐」、ピラミッドのような「角錐」は「錐体」。そして、ボールのような「球体」がありましたね。
これらの「かさ」(体積)や「外側の面積」(表面積)を計算する方法を学びました。
- 体積(かさ)の求め方:
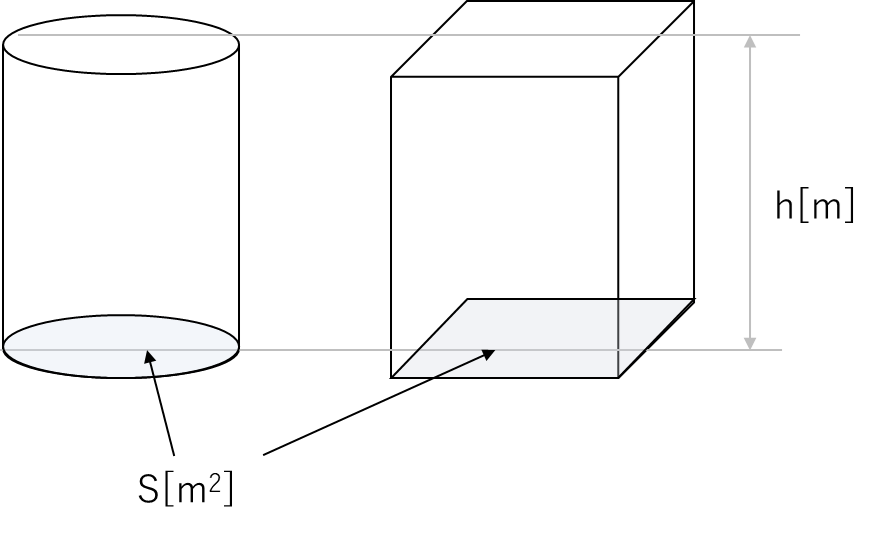
- 柱体(円柱、角柱など): 底面の面積 × 高さ(図1)
- (例:牛乳パックの底の面積に、高さをかけると牛乳の量(体積)がわかる)
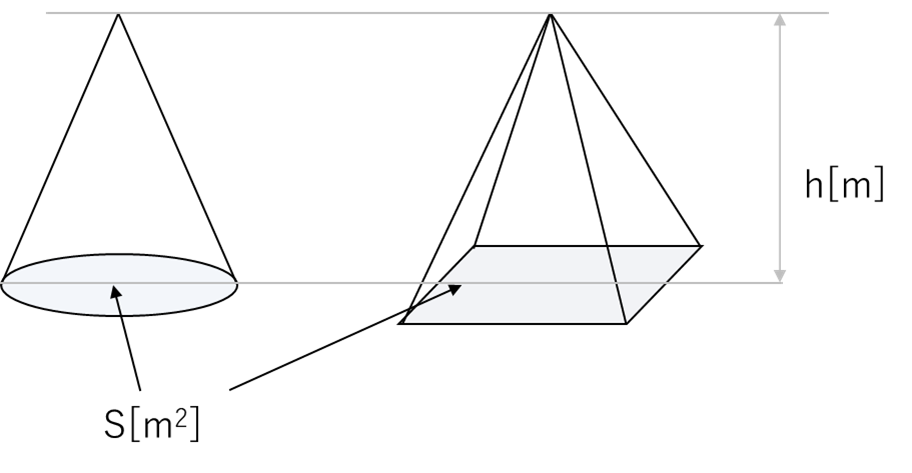
- 錐体(円錐、角錐など): 底面の面積 × 高さ × 1/3(図2)
- (柱体と同じ底面積・高さでも、先が尖っている錐体は柱体のちょうど1/3の体積になる)
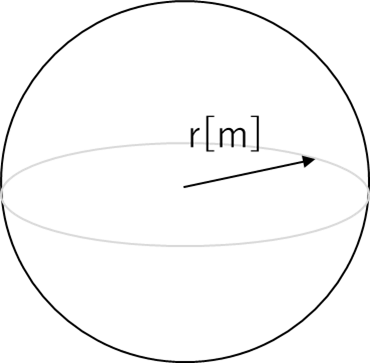
- 球体(ボールなど): (4/3) × 円周率(π)× 半径 × 半径 × 半径(図3)
- (πを使う計算で、ちょっと大変だった記憶がある方もいるかも?)
- 柱体(円柱、角柱など): 底面の面積 × 高さ(図1)
- 表面積(外側の面積)の求め方:
- それぞれの図形を展開図にしたりして、全ての面の面積を合計する方法を学びました。例えば、円柱なら側面の長方形と上下の円2つの面積を足す、といった具合です。
空間図形が「社会で役立つ」って、具体的にどんな場面?
「公式、なんとなく思い出したけど、これがどう社会と繋がるの?」ここからが本番です!
場面1:ものづくりの材料を計算する
何かものを作る時には、必ず材料が必要です。この「どれだけ材料が必要か」を計算するのに、空間図形は大活躍します。これは、ものづくりのコストに直結する、とっても重要な計算なんです。
- 金属の塊の体積計算:
- 例えば、自動車の部品や色々な製品の材料となる「金属の塊(ビレットと呼ばれます)」があります。 図4.アルミビレット(本多金属工業HPよりイメージ)
- この金属の塊を加工して製品を作る場合、まず「この塊1本で、どれくらいの体積の材料があるか」を正確に計算する必要があります。それが分かれば、「製品を100個作るのに、この塊が何本必要か」という全体の材料の量を計算できます。
- もしこの体積計算を間違えると、材料が足りなくなったり、逆に無駄に買いすぎてしまったり… ビジネスでは大きな損失に繋がってしまうこともあります。
- 塗料の体積計算:
- 製品の表面に色を塗ったり(カラーリング)、錆びないようにメッキを施したりする工程も、広い意味で「塗装」です。この「塗料」がどれだけ必要か計算するのにも、空間図形が使われます。
- 塗料は、製品の「表面」に薄い膜として塗られますよね。この薄い膜の「体積」を計算したいとき、原理は「底面積×高さ」と同じです。ここでいう「高さ」は塗料の膜の薄さ、「底面積」は、塗る対象物の「表面積」にあたります!
- そう、製品の「表面積」が正確に計算できないと、塗料の必要な量も分からず、無駄が出たり、逆に足りなくなったりしてしまいます。私たちが何気なく見ている製品の色や質感も、その裏では空間図形の知識が活きているんですね。


場面2:水や空気の流れをデザインする
お家で水道の蛇口をひねったり、庭に水を撒くためにホースを使ったりしますよね。流れる水の量や勢いをコントロールするには、空間図形の考え方が役立ちます。
これはまさに「底面積(断面積)× 高さ(1秒間に進む長さ=流れる速さ)」という、柱体の体積を計算する考え方そのものです。水道やガスが安全に、そして必要な量だけ届くように設計する裏側にも、空間図形の知識が使われているんですね。
流量(流れる量)の計算
水道管やガス管、工場で材料を運ぶパイプの中を流れる水や空気、ガスなどの量(「流量」といいます)は、「1秒間にどれくらいの量が流れているか」で表されます。
この流量は、「流れる速さ」と、管の「太さ」(断面積)で決まります。
流量 = 流れる速さ × 管の断面積
例えば、管の断面が丸い(円形)なら、断面積は円の面積の公式「円周率 × 半径 × 半径」で計算できます。そして、「流れる速さ」にこの「断面積」をかけると… 単位を見てみると【m/秒 × m² = m³ /秒】となり、「1秒間にm³(立方メートル)の量が流れる」、つまり「流量」が計算できるんです!
場面3:目に見えない電気の「強さ」を考える
電気や磁力のように、目には見えないけれど確かに存在し、私たちに影響を与えるものがあります。空間図形は、このような目に見えないものの「強さ」を考えるときにも顔を出します。
電界(電気の場)の強さの計算
- プラスやマイナスの電気を帯びたものの周りには、「電界」という目に見えない場ができています。この電界は、他の電気を帯びたものに力を及ぼします。
- この電界の「強さ」を考えるときに、「電気力線」という、電気の力がどのように広がっているかを示す仮想の線を使ってイメージすることがあります。
- プラスの電気からは、このように放射状に(全ての方向に均等に)線が出ているイメージです。
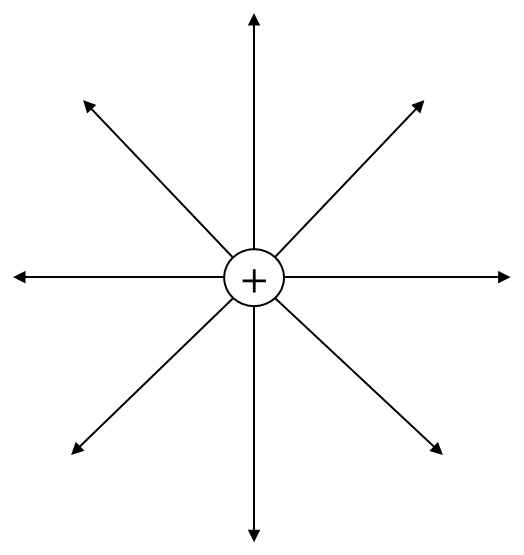
- この線が密集している場所ほど電界が強く、線がまばらになっている場所ほど電界が弱い、と考えます。
- では、プラスの電気から遠ざかるにつれて電界の強さがどう変わるかを計算するにはどうしたらいいでしょう? ここで空間図形が登場します。
- プラスの電気の周りに、それを中心とした大きな球体を想像してみてください。プラスの電気から出る線は、この球体の表面を突き抜けて広がっていきます。
- 遠くに行くほど線がまばらになるのは、線が進むにつれて「通過する面積」がどんどん大きくなるからです。この「通過する面積」として、球体の「表面積」が使われるのです!
- 電界の強さは、出る電気力線の総数を、その広がる面積(例えば球の表面積)で割った「線(力)の密度」で考えることができます。電荷から距離rの場所での電界の強さを計算する際に、分母に半径rの球の表面積「4πr²」が出てくるのはこのためです。
- 「こんな計算が社会でどう役立つの?」と思われるかもしれませんが、例えば頭の上を通っている送電線の周りの電界の強さを計算したり、電子機器が発する電磁波の影響範囲を考えたりする際に、このような「目に見えない場の強さを空間的に捉える」という考え方が基礎になります。

まとめ:「社会で使うの?」への答えと、子どもの未来への繋がり
中学1年生で習う空間図形の体積や表面積の計算は、単なるテストのための公式ではありませんでしたね。
ものづくりの現場で材料の無駄をなくしたり、水道やガスを安全に届けたり、そして目に見えない電気や電波の性質を理解したり… 私たちの暮らしを支える様々な場所で、そして将来お子さんたちが関わるであろうAIやIoTといった最先端技術の基礎となる物理現象を理解するためにも、空間図形は「生きた知識」として役立っています。
「こんなん、社会に出てから使う機会あるの?」という疑問は、子どもたちが学習する上で当然湧いてくるものです。そんなとき、「そうだよ!例えば、君が毎日使っている〇〇(身近な製品)の裏側で、この空間図形の考え方が使われているんだよ」と、具体的な例を挙げて教えてあげられたら、子どもたちの学びへのモチベーションも変わってくるかもしれません。
空間図形の知識は、目に見えるものだけでなく、見えない世界の広がりや、ものごとの繋がりを理解するための「物の見方」を与えてくれます。ぜひ、日常の中で「これはどんな形かな?」「かさはどれくらいかな?」と、お子さんと一緒に空間図形探しを楽しんでみてください。きっと、学びの楽しさや探求心に繋がるはずです。