私たちの生活の中には、「温度を一定に保つ」技術があふれています。エアコン、炊飯器、こたつ、ホットカーペット、冷蔵庫……こうした家電製品は、ただ熱を加えたり冷やしたりしているだけではありません。実は、それぞれが精密な温度制御の仕組みによって「ちょうどいい温度」を維持しているのです。
今回は、そんな温度制御の仕組みについて掘り下げてみましょう。
- 温度を一定に保つために必要な基本要素(センサー・制御装置・加熱装置など)
- 温度制御の仕組みと代表的な制御方式(オンオフ制御・PID制御)
- 制御を理解するための基本的な数学的考え方(フィードバック、比例制御など)
- ホットカーペットや冷蔵庫、半導体製造装置など、身近な温度制御の応用例
1. 温度を一定に保つために必要な要素とは?
「一定の温度を保つ」と聞くとシンプルに聞こえますが、それを実現するにはいくつかの重要な構成要素が必要です。
センサー(測る)
まず必要なのは、現在の温度を測定するセンサーです。サーミスタや熱電対など、さまざまな種類の温度センサーがあります。

アクチュエーター(加熱・冷却)
次に、温度を変化させるための装置が必要です。・・・というと大げさですが、暖房やクーラー、冷蔵庫に電子レンジなど、温めたり冷やしたりする機器のことを言っています。
制御装置(判断する)
そして最も重要なのが、センサーの値をもとに加熱・冷却の度合いを決める「頭脳」の部分。これが制御装置です。
2. 温度制御の基本的な仕組み
温度制御は、簡単に言えば「今の温度」と「目標の温度」を比較して、その差に応じてヒーターなどをON/OFFしたり、加熱量を調整したりする仕組みです。
ON/OFF制御(サーモスタット)
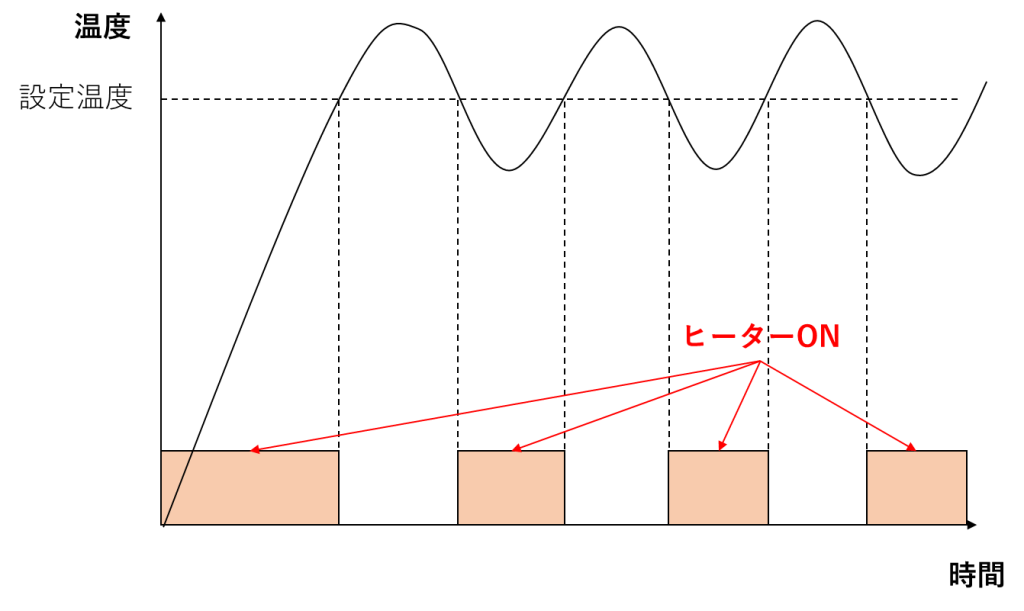
もっとも単純な方法は「ON/OFF制御」です。設定温度より低ければ加熱をON、高ければOFF。この仕組みはホットカーペットや便座ヒーターによく使われます。構造が簡単でコストも安く済みますが、温度が上下にゆらぎやすいという特徴があります。
グラフにすると、こんな感じで表されます。オレンジの枠で示している時間範囲でヒーターをONにすると、下降していた温度が再び上昇に転じることが見て取れるかと思います。
PID制御(比例・積分・微分制御)
より精密な制御を実現するために使われるのがPID制御です。これは、次の3つの要素を組み合わせて出PID制御とは、たとえばエアコンや炊飯器などで「設定温度」にうまく到達するように、ヒーターの出力やファンの風量などを自動でなめらかに調整してくれる仕組みです。
その名の通り、3つの要素で成り立っています。
P(比例:Proportional)
今の「目標とのズレ(=誤差)」が大きければ、それに比例した力で調整します。
たとえば部屋が冷えすぎていれば、強めに暖房。あと少しなら弱めに、というイメージ。
- 数式: P = Kp × e(t)
(e(t):今の誤差)
I(積分:Integral)
過去にちょっとずつズレていた誤差をコツコツ蓄積して補正します。
たとえば「ずっと設定よりちょっと低いまま」なら、それを見て少し強めに暖房をかける感じです。
- 数式: I = Ki × ∫e(t)dt
(過去の誤差を積分)
D(微分:Differential)
誤差がどのくらいのスピードで変わっているかを見て、先回りして効きすぎを防ぐ役割。
たとえば、急に設定温度に近づいてきたら「もうそろそろ止めとくか」とブレーキをかけるイメージです。
数式: D = Kd × de(t)/dt
(誤差の変化率を微分)
たとえば、こんな感じのグラフになります。先ほどのON/OFF制御とは違って、設定温度周りでの温度の上下動がないことがわかります。

3. 制御を理解するための数学的な視点
制御のしくみを理解するうえで、高校~大学初級レベルの数学が大きな助けになります。ここでは代表的な考え方をいくつか紹介します。
フィードバック(負帰還)の基本式
温度制御では、「今どれくらい目標値とズレているか?」をもとに制御量を調整します。これが負帰還(ネガティブ・フィードバック)です。
たとえば、
- 設定温度:${T_{set}}$
- 現在の温度:${T(t)}$
とすると、誤差(エラー)は ${e(t)=T_{set}-T(t)}$
この誤差をもとに、加熱・冷却の強さを決めていきます。
時間とともに変わる量 → 微分・積分の世界へ
温度制御では、単に「ズレがある」だけではなく、
- ズレがどれくらい続いているか(=積分)
- ズレがどのくらい急に変化しているか(=微分)
を考慮すると、より滑らかで的確な制御ができます。
これを実現するのが PID制御です。
数式では、出力(操作量)u(t)を以下のように表します:
${u(t)= K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \frac{de(t)}{dt}}$
- ${K_p}$:比例(P)ゲイン
- ${K_i}$:積分(I)ゲイン
- ${K_d}$:微分(D)ゲイン
このように、比例・積分・微分の3要素がバランスよく組み合わさることで、目標温度に向かって素早く・安定して・行き過ぎずに到達できるのです。
シミュレーションで体感できる
この制御モデルは、実際にExcelやPythonなどでシミュレーションすることも可能です。
たとえば、温度がどのように時間とともに変化するかを簡単なモデルで試すだけでも、「数学がどう制御とつながるか」が体感できます。
制御は「時間軸上の賢い調整」
制御とは、単なる現在値の調整ではなく、
- 「過去の蓄積(I)」
- 「現在の状況(P)」
- 「未来の予測(D)」
をもとに、時間の流れに沿って判断を下す技術です。
この時間軸の扱いこそ、微分方程式やフィードバック理論といった数学の役割が大きくなるポイントなのです。
4. 温度制御の応用事例
最後に、私たちの身の回りにある温度制御の応用事例をいくつか見てみましょう。
炊飯器:ご飯を「蒸らす」まで制御
炊飯器は、炊く→蒸らす→保温という工程を通じて、時間と温度を緻密に制御しています。近年ではマイコン制御によって、米の種類に合わせた最適な温度プロファイルが実現されています。
冷蔵庫:庫内温度を一定に保つ
冷蔵庫では、庫内の温度を一定範囲に保つために、センサーが常時監視し、コンプレッサーのON/OFFやファンの回転数を調整しています。
3Dプリンタやリフロー炉:産業用途でも活躍
産業分野でも温度制御は重要です。3Dプリンタではノズル温度が一定でなければ樹脂が適切に溶けず、リフロー炉でははんだが正しく溶ける温度管理が必要です。
おわりに
温度制御は、一見地味ですが、実は生活を支える縁の下の力持ち。仕組みを知ることで、家電の使い方にも理解が深まり、ものづくりへの応用アイデアも広がります。
今後、身の回りのモノを見るとき、「これってどうやって温度制御してるんだろう?」という視点を持ってみると、新しい発見があるかもしれません。


